It is a measure of inequality developed by the Italian statistician Corrado Gini and published in 1912. It varies from 0 to 1; 0 corresponds to complete equality and 1 corresponds to complete inequality. We use the GINI index to measure the inequality in the rabbit calorie distribution.

-Gini coefficient was higher for the heterogeneous landscapes, demonstrating that unequal distribution of resources increases competition among rabbits leading to inequality.

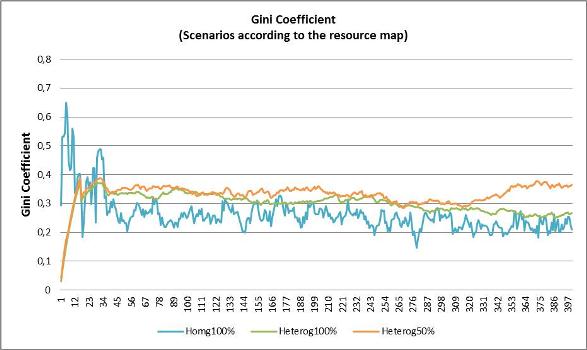Gini Coefficient in three different landscapes: Hom 100- with resources distributed homogeneously, Het 100-with the same amount of resources distributed heterogeneously and Het 50-with half of resources amount distributed heterogeneously

-The agent population stabilizes regardless of the distribution of resources on the landscape and the amount of resources consumed by each agent according to the group to which it belongs.

Number of agents in three different landscapes: Hom 100- with resources distributed homogeneously, Het 100-with the same amount of resources distributed heterogeneously and Het 50-with half of resources amount distributed heterogeneously.
The graph shows that in the three scenarios there is a rapid growth in the first steps of the model followed by a decrease in amount of agents when the first 200 rabbits die almost at the same time because of their same age. Thus the three populations stabilize in different ways.

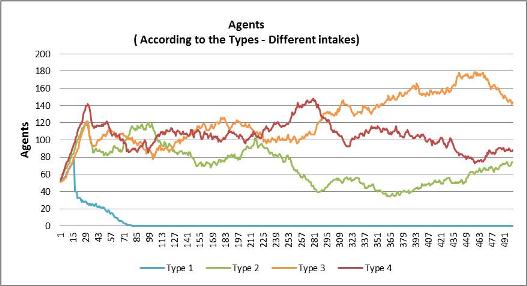Number of agents, using Hetererogeneous 100 landscape map, divided by different Maximum absorption capacity of resources according to the groups to which each agent belongs. In this case: Type 1 (17 calories), type 2 (19 calories), type 3 (22 calories) and type 4 (25 calories).
Only type 1 group that eats much less than needed to survive had its population extinct from starvation, considering that it had exhalted its calorie stock to survive in few steps. Type 2 group also eats less than it needs to survive has to use its stock to survive. But the depletion of its stock was not enough to cause its death from starvation before “natural” age death. The other two groups eat more than they need to survive and accumulate calories, but the model doesn't have any rule that favors rabbits with bigger stocks of calories in the birth process. Hence the populations of all groups grow differentialy based only on their death rates.

-There are many more deaths from starvation on heterogeneous landsacapes and this number is higher in scenarios with less amount of resources.

In the three scerarios, There are many deaths in the first steps of the model. This is due to the deaths of Type 1 rabbits, which eat much less than they need to survive. After the step, there are no deaths from starvation in homogeneous scenario and most of the deaths occour on the heterogeneous landscape scenario with half amount of resources. This is due many to rabbits that are born in areas with few resources, hence they cannot accumulate energy and waste their stock and thus die from starvation.

-The amount of resources available stabilizes as the population also stabilizes leading the amount of resources consumed to a dynamic equilibrium.

Videos show rabbits position map and landscape maps under the three different scenarios

The black points are the agents moving across the landscape that is represented using color scale according to the amount of resources. Red represents larger amount of resources, and blue otherwise.

Homogeneous scenario: every cell has the same value in this map: 100 - average cell value: 100 -

Heterogeneous scenario: cells have values from 0 to 147 - average cell value: 100 -

Heterogeneous scenario: cells have values from 0 to 73 - average cell value: 50 -

On heterogeneous landscapes, the agents move to locations with larger concentration of resources. As a result, this areas are depleted first.

Back to Home

Next section

ABM of population dynamics can provide insights about how individuals are affected by the characteristics of the matrix in which they are inserted (Nathan et al., 2008; McLane et al., 2011).

ABM highlights the causal relationships among movement, individual attributes and internal state, demographic and the environment. Analysis of these interactions help understanding the emergence of patterns such inequality due to greater competition resulting from paucity of resources.